ECE 252

Week 1

Universal Compute

1. Turing Machine: any computable computation can be implemented by some machine
2. Universal Turing Machine: A programmable computer is effectively a Universal Turing Machine (minus infinite memory).
3. A computer can compute anything that’s possible to compute given enough memory and time.
4. Design trade-off: Time, Cost, Power/Energy.

Complexity

1. 1st transistor -> Bell Labs, 1st IC -> Jack Kilby(MSEE’50), 1st microprocessor -> Intel
2. Moore’s Law: number of transistors on a microchip doubles approximately every two years(24 month). -> Cost halves every two years.

Abstraction

1. Use abstraction to manage complexity.
2. The ISA lies at the software/hardware boundary.
3. Problem Statement –Software Design–> Algorithm –Programming–> Program –Compilation–> ISA –Processor Design–> Microarchitecture –Logic/Circuit Design–> Logic Circuits –Implement&Fabricate–> Devices

Electral Infomation

1. Analog: continuous range of values
2. Digital: discrete set of values (almost all eletronic device)
3. In reality, the voltage levels are actually ranges of voltages.
4. Voltage = Current * Resistance
5. Any data processed by a digital computer is represented by sequences of 1s and 0s

Week 2

Number representation

1. demical-10, Binary-2, Octal-8, Hexademical-16
2. least-significant, right most; most-significant, left-most
3. $D_{N-1}\cdots D_{1}D_{0}=D_{N-1}*r^{N-1} + \cdots + D_{1}r^1 + D_0r^0$
4. Each position represents a power of base; Digital value says how many of that power of base.
5. A value is a particular quantity, a number is a way to represent a value. Same “number”, different value.

Base conversion

1. Binary <-> Hex: directly substitute a hex digit for a 4-bit binary number.
2. Binary <-> Octal: directly substitute a octual digit for a 3-bit binary number.
3. Octal <-> Hex: use binary as an intermediate form.

Arithmetic

1. Substraction using borrowing: If necessary, bowrrow the base’s value from one position higher
2. Multiple by power of base, shifts number to the left. Divide by power of base, shifts numbers to the right.

Signed Numbers

1. Signed-Magnitude: The most significant bit is the sign, the remaining bits are the numbers magnitude.
2. 2’s Complement representation: positive numbers start with 0, negative numbers start with 1 ($-2^N$).
3. Fast Negation: complement each bit and the add 1.
4. Addition: works the way it does for unsigned binary number except the carry-out is not meaningful.
5. Substraction: add the negation of the value we wish to subtract
6. Operand/Result bitwidths match: operands and results must have the same number of bits for the math to work correctly.

Sign Extention

1. Extend 2’s complement number: for positive: zero-extension; for negative: one-extension
2. Negative 1 in 2’s complement: $-1\cdots1$
3. Unsigned number: $[0, 2^n -1]$, signed number: $[-(2^{n-1}-1), 2^{n-1}-1]$, 2’s-complement number: $[-2^{n-1}, 2^{n-1}-1]$
4. Overflow: The result cannot be correctly represented in the required number of bits.
5. lf adding two negative 2’s-complement numbers overflows, the sign of the result will appear to be non-negative.
6. lf the result of adding two positive 2’s-complement numbers appears to be positive, then the operation did not overflow.
7. lf adding two unsigned numbers overflows , the result will appear to be
   smaller than it should be.

Week 3

Fixed Float

1. Radix point: separates the integer portion from the fractional portion of the numebr
2. when the format defines a “fixed” position for the radix point within the number’s digits
3. 
4. Shifting right by $N$ bits is equivalent to dividing by $2^N$
5. location of radix is not visible, not encoded in the number, must told. We never know the meaning of a binary number just by looking at it.

Floating Float

1. 
2. 
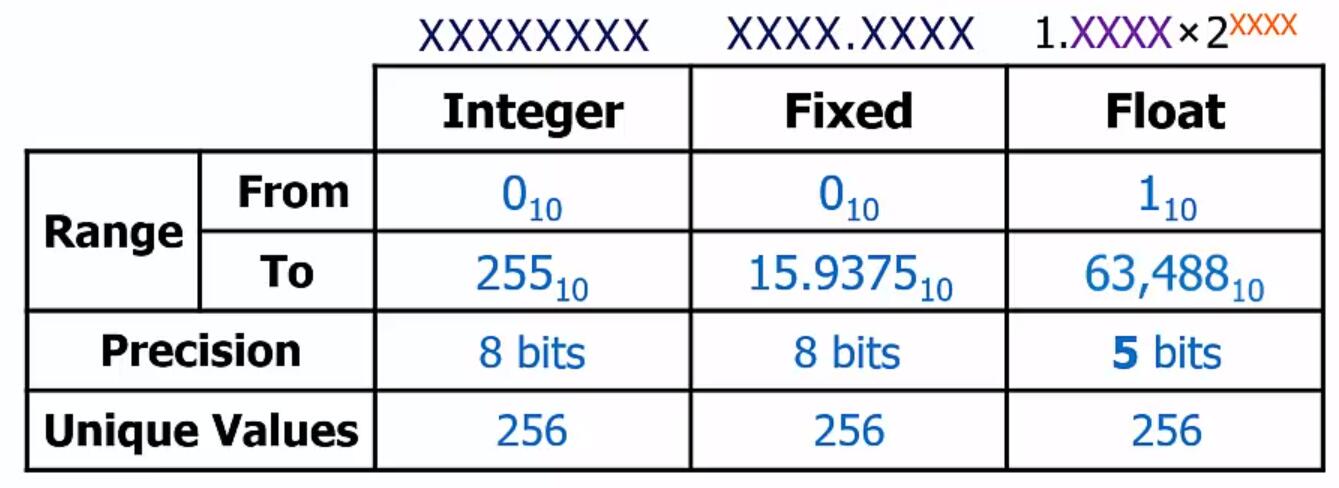
3. Precision: number of significant digits. No need to transform 10.

ASCII

1. 7 bits to represent 128 different characters.
2. UTF-8, 16, 32

Week 4

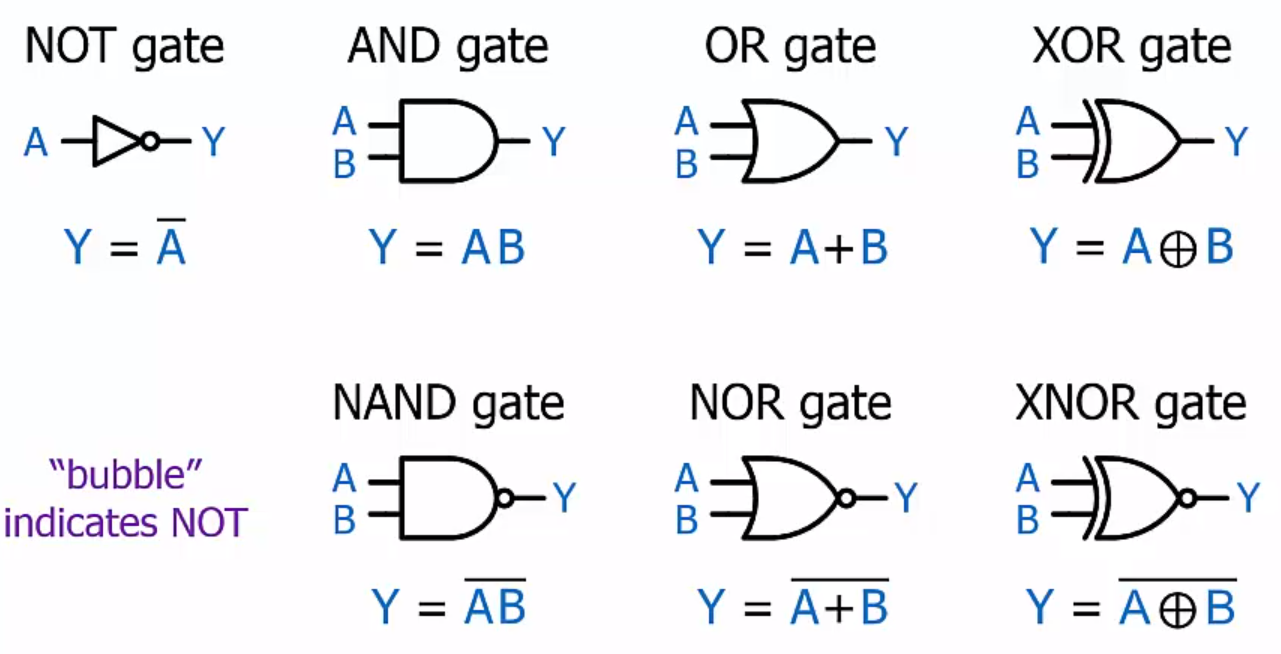
Logic Functions

1. AND: result is true if all operands are true
2. OR: result is true if any operand is true
3. NOT: result is the opposite of the operand value
4. 
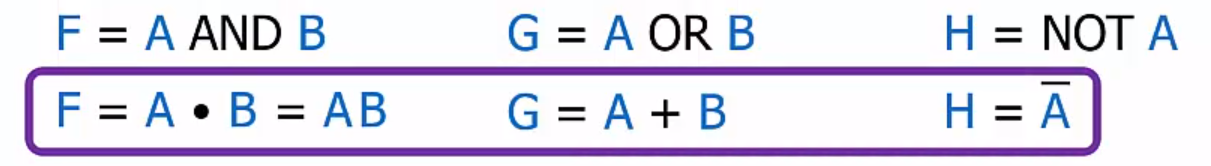
5. XOR: the result of a two-operand OR is true if both operands are true, the odd function
6. A bitwise operation computes each bit of an N-bit result based on the value in the correponding position of the N-bit operands.

Combiational Logical

1. 
2. 
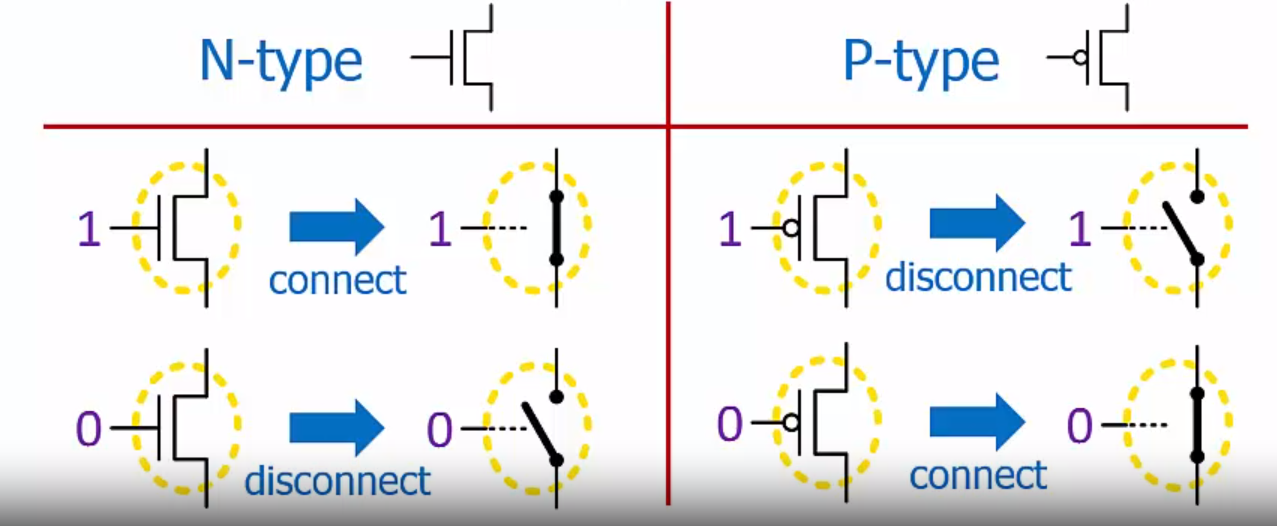
3. Waveforms: a waveform is a visual way to represent signal values over time.
4. Logic circuits are at a higher level of abstraction. Each transistor acts like a switch.
5. NOT gate use 2 transisters.

Combinational Blocks

1. Decoder: converts an n-bit input code word into a unique m-bit ouput value, where $m=2^n$.
2. Exactly one output can be true at any given time.
3. 
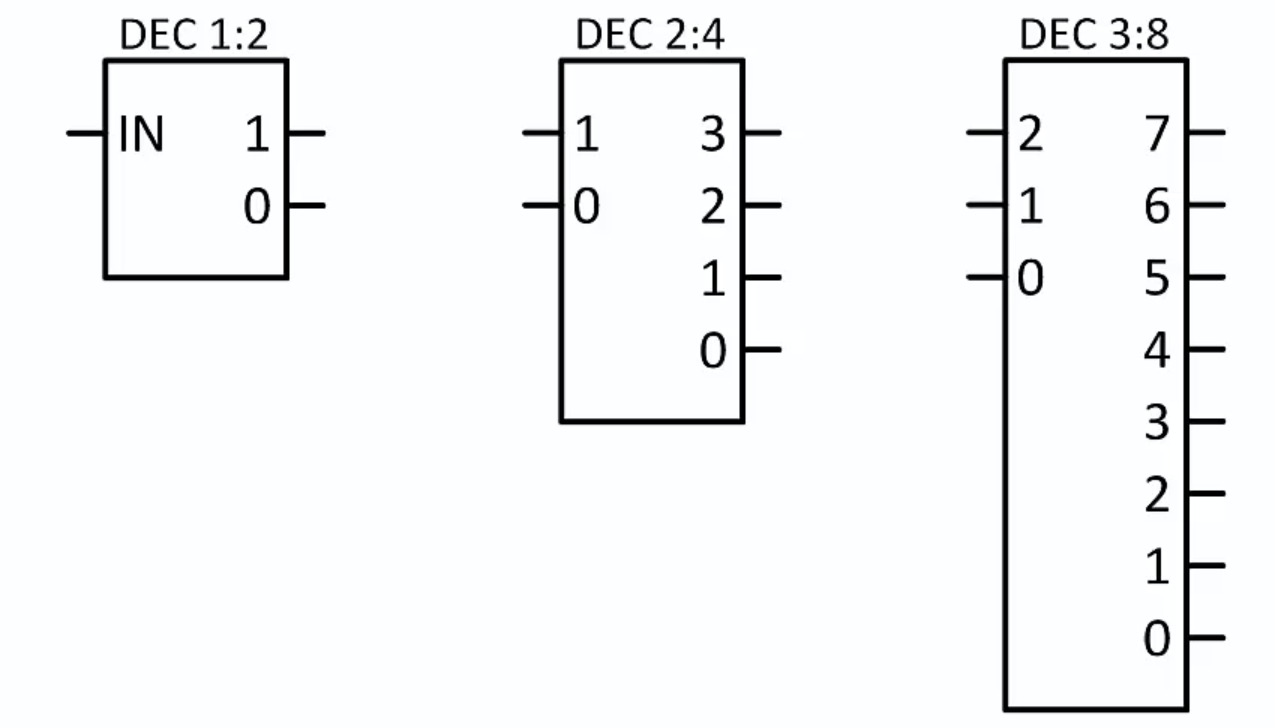
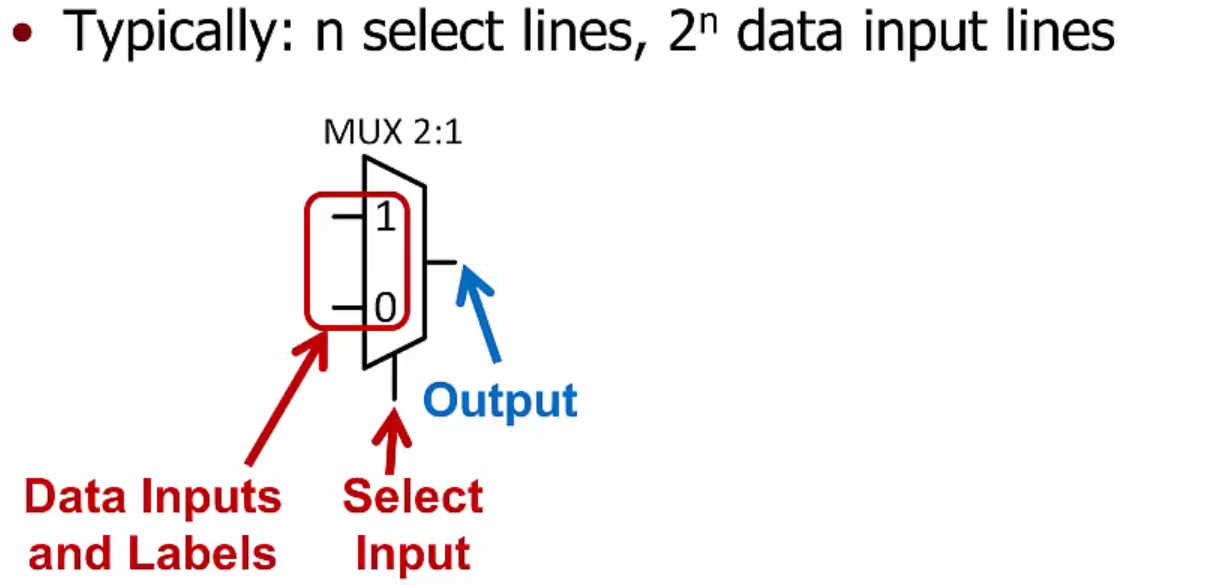
4. Multiplexers: based on the select input, choose one of the data inputs to drive the output
5. 
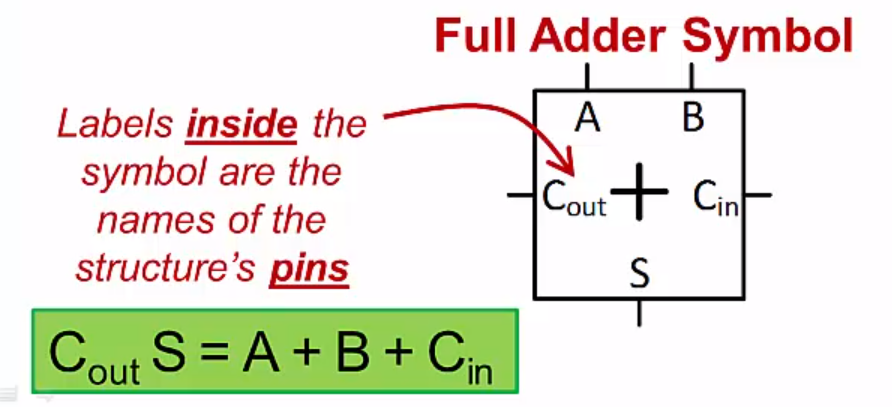
6. Full adder: at every position, determine 2-bit sum of adding each addend’s bit in that position plus a carry-in. A full adder performs addition for single bit position.
7. 
8. Ripple Carry Adder: serires of full adders, where each full adder performs the addition for a single bit position.

Week 5

Sequence Logic

1. Before, are all combinational logic. Circuit outputs only depend on current input values.
2. A circuit’s current state is the binary number that is currently stored in the circuit’s flip-flops.
3. Sequence logic: circuit outputs depend on both current input values and past stored values.
4. D flip-flop: output is always equal to the value it is storing
   
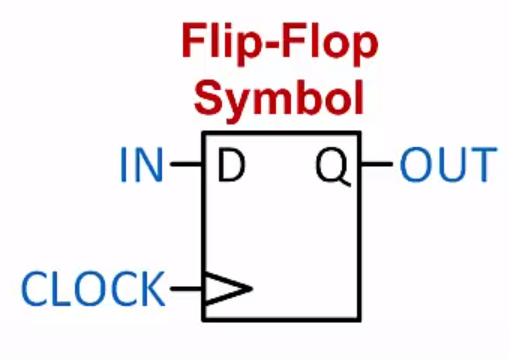
5. D flip-flop updates when the clock transitions from 0 to 1 (rising edge)
6. FSM (finite state machine): any circuit built from flip-flops is FSM
7. State Diagram:
   1. state is represented by a circle, the circle also indicate the output in that state.
   2. state transitions represented by an arrow from one state to another. Labeled with the input condition.

FSM

1. sequential circuits.
2. track of which state it is currently in
3. The FSM contains one flip-flop per bit of state
4. depends both upon the current state and the inputs, the next state is a function of the current state and current input values.
5. Start state <-> reset state
6. Some state machines do not have an input, or the input does not affect a particular state transition, this type of transition is an unconditional transition.
7. “X” means shorthand for “any value of”
8. The output will be the current state output.

Registers Memory

1. A register is a group of flip-flops used to stire multi-bit binary values.
2. Write-Enable: whether take the input to store
3. Address: M bits, $2^M$ locations to access.
4. Each location stores a single N-bit word: data size, # bits per location
5. Capacity = (# locations) * (data size)
6. Address selects which register supplies data out using Mut.
7. Address selects which register may be written to using decoder. Selected register will only be written if WE=1

Week 6

1. ALU(arithmetic logic unit), a set of logic structures that perform a set of different possible computations on the inputs.
2. A set of multiplexers that choose which result to send to the ALU output.
3. The register file: a small memory located near the ALU
   write port: used to write operation’s result to register file: DR(DA), DD(DD), write
   read port: used to get operands from register file: SR(SA), SD, BMUX, output
4. Conceptual Compute Model: Memory, Control Unit, Processing Unit
5. Control Unit: fetches instructions one by one from memory, two special unit PC(program counter), IR(instruction register). Memory read using address in PC, put the returned value into IR, then increment the PC.
6. von Neumann Compute Model, holds both the program and any data needed by the program(memory)
7. Instruction: small step of a program is encoded into a binary word called an instruction. (ISA)
8. FETCH: Read an instruction from mem, put into IR and increase PC
   -> DECODE: determine what the instruction meaning (opcode, field)
   -> EVALUATE ADDRESS
   -> FECTCH OPERANDS: get the operands
   -> EXECUTE: ALU
   -> STORE RESULT: write back to register
   repeat forever, not all phases are required for all instruction(后四个)
9. Some processors group different stage together

Week 7

1. LC-3: 8 general-purpose registers, 16 bit
2. N, Z, P: three branch bit reg
3. address calculation method depends on the memory addressing mode.
4. Mem both holds ins and data